April 25, 2010
Douglas Holmes
COMP510
Spring 2011
Assignment 6
22.2-1) Show the d and π values that result from running breadth-first search on the directed graph of Figure 22.2(a), using vertex 3 as the source.
Using vertex 3 as a source, the d and π values are as follows:
| d | π |
|---|
| 1 | ∞ | Ø |
| 2 | 3 | 4 |
| 3 | 0 | Ø |
| 4 | 2 | 4 |
| 5 | 1 | 3 |
| 6 | 1 | 3 |
22.2-2) Show the d and π values that result from running breadth-first search on the undirected graph of Figure 22.3, using vertex u as the source.
Using vertex u as a source, the d and π values are as follows:
| d | π |
|---|
| r | 4 | s |
| s | 3 | w |
| t | 1 | u |
| u | 0 | Ø |
| v | 5 | r |
| w | 2 | t,x |
| x | 1 | u |
| y | 1 | u |
22.2-6) There are two types of professional wrestlers: "good guys" and "bad guys." Between any pair of professional wrestlers, there may or may not be a rivalry. Suppose we have n professional wrestlers and we have a list of r pairs of wrestlers for which there are rivalries. Give an O(n + r)-time algorithm that determines whether it is possible to designate some of the wrestlers as good guys and the remainder as bad guys such that each rivalry is between a good guy and a bad guy. If is it possible to perform such a designation, your algorithm should produce it.
The algorithm, as described in reference 3:
BFS(G)
for each vertex w ∈ G.V
w.wrestler = GOOD
ENQUEUE(w)
end
while ENQUEUE ≠ ∅
u = DEQUEUE(w)
for each v ∈ G.Adj[u]
if v.wrestler == w.wrestler end
//no rivalry because same wrestler
elseif v.wrestler != w.wrestler
if v.wrestler != GOOD
v.wrestler = BAD
ENQUEUE(v) //insert wrestler as a bad wrestler
end
elseif v.wrestler == GOOD
v.wrestler = GOOD
ENQUEUE(v) //insert wrestler as a good wrestler
end
end
elseif v.wrestler != GOOD & v.wrestler != BAD & v.wrestler!= w.wrestler
v.wrestler = NORIVAL
ENQUEUE(v) //insert wrestler into queue as neither
end
end
end
u.wrestler = COMPLETE
Essentially, we create a graph of wrestlers and assign each vertex as good while placing them all in a queue. As we pull each wrestler from the queue, we check adjacent wrestlers to see if they're good or bad, then if they're opposed set them as rivals. The queue ends when it's marked COMPLETE, and the time it takes to get there is O(n + r) because we have to go through all n wrestlers and r rivals.
22.3-11) Show that a depth-first search of an undirected graph G can be used to identify the connected components of G, and that the depth-first forest contains as many trees as G has connected components. More precisely, show how to modify depth-first search so that each vertex v is assigned an integer label cc[v] between 1 and k, where k is the number of connected components of G, such that cc[u] = cc[v] if and only if u and v are in the same connected component.
Using the following modified DFS algorithms from reference 4:
DFS(G)
for each vertex u Î V[G]
do color[u] ¬ WHITE
p[u] ¬ NIL
cc[u] ¬ 0
componentNo ¬ 1
time ¬ 0
for each vertex u Î V[G]
do if color[u] ¬ WHITE
then DFS-VISIT(u, componentNo)
componentNo ¬ componentNo + 1
DFS-VISIT(u, componentNo)
color[u] ¬ GRAY
cc[u] ¬ componentNo
time ¬ time + 1
d[u] ¬ time
for each v Î Adj[u]
do if color[v] = WHITE
then p[v] ¬ u
DFS-VISIT(v, componentNo)
color[u] ¬ BLACK
f[u] ¬ time ¬ time + 1
Using theorem 22.10 from the 2nd edition of the textbook, we know that every edge of G is a tree or back edge. Because it's an undirected graph, the result set of sub-graphs doesn't depend on the order that we examine the vertices. If we want to identify the connected components of G, we have to assign an integer label to each connected component, where vertices of each component will have equal values.
22.4-1) Show the ordering of vertices produced by TOPOLOGICAL-SORT when it is run on the dag of Figure 22.8, under the assumption of Exercise 22.3-2.
| m | n | o | p | q | r | s | t | u | v | w | x | y | z |
|---|
| d | 1 | 21 | 22 | 27 | 2 | 6 | 23 | 3 | 7 | 10 | 11 | 15 | 9 | 12 |
| f | 20 | 26 | 25 | 28 | 5 | 19 | 24 | 4 | 8 | 17 | 14 | 16 | 18 | 13 |
Which gives a solution of:
p -> n -> o -> s -> m -> r -> y -> v -> x -> w -> z -> u -> q -> t
22.5-1) How can the number of strongly connected components of a graph change if a new edge is added?
If a new edge is added, one of two things could happen. If the new edge connects two vertices that belong to a strongly connected component, the number of strongly connected components will remain the same. If, instead, the edge connects two strongly connected components, and the edge is in the reverse direction of an existing path between the two components, then a new strongly connected component will be made, increasing the number of components.
22.5-2) Show how the procedure STRONGLY-CONNECTED-COMPONENTS works on the graph of Figure 22.6. Specifically, show the finishing times computed in line 1 and the forest produced in line 3. Assume that the loop of lines 5-7 of DFS considers vertices in alphabetical order and that the adjacency lists are in alphabetical order.
STRONGLY-CONNECTED-COMPONENTS asks us to compute the finishing times for each vertex using DFS, compute the graphs transpose, then call DFS on the transpose considering the finishing times of the graph.
So first, we need the finishing times:
| q | r | s | t | u | v | w | x | y | z |
|---|
| d | 1 | 17 | 2 | 8 | 18 | 3 | 4 | 9 | 13 | 10 |
| f | 16 | 20 | 7 | 15 | 19 | 6 | 5 | 12 | 14 | 11 |
Then, we need to compute the transpose:
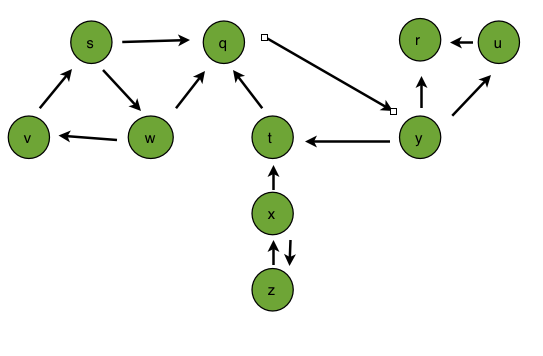
Finally, we need the finishing times of the transpose with respect to the original finishing times:
| q | r | s | t | u | v | w | x | y | z |
|---|
| d | 5 | 1 | 15 | 7 | 3 | 17 | 16 | 11 | 6 | 12 |
| f | 10 | 2 | 20 | 8 | 4 | 18 | 19 | 14 | 9 | 13 |
Giving us the following components:
{r} -> {u} -> {q, y, t} -> {x, z} -> {s, w, v}
22.5-3) Professor Deaver claims that the algorithm for strongly connected components can be simplified by using the original (instead of the transpose) graph in the second depth-first search and scanning the vertices in order of increasing finishing times. Is the professor correct?
No, because the components will not be the same if we calculate with the normal graph. Using the example above, lets run step 3 as Professor Deaver describes:
| q | r | s | t | u | v | w | x | y | z |
|---|
| d | 12 | 19 | 2 | 13 | 17 | 3 | 1 | 8 | 11 | 7 |
| f | 15 | 20 | 5 | 14 | 18 | 4 | 6 | 9 | 16 | 10 |
Giving us a completely different set of strongly connected components as a result.
References:
- Course Textbook: T. Cormen, C. Leiserson, R. Rivest, C. Stein. Introduction to Algorithms, Second Edition.
- Course Textbook: T. Cormen, C. Leiserson, R. Rivest, C. Stein. Introduction to Algorithms, Third Edition.
- For question 22.2-6: http://putzing-around.blogspot.com/2007/10/from-my-algorithms-textbook-22.html
- For question 22.3-11: http://csuci.mathworld.info/26.html
